AC自动机

朴素做法

AC自动机，是用于处理一个主串与多个模式串匹配的算法，kmp就是AC自动机的一个特例（只有一个模式串的AC自动机），即单串自动机。

而多个模式串需要用 Trie 来组织，所以AC自动机就是 Trie+kmp。

画图说明，下面是单词集{she,shr,say,he,her} 的 Trie 树：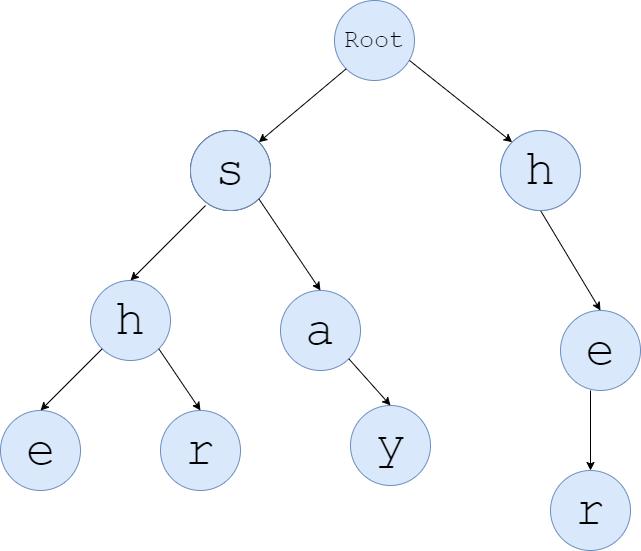

如果我们想查找主串yasherhs与哪些模式串匹配，朴素做法是这样的：

1. 看第一个字符y，Trie 中没有根到y的边，跳过；
2. 看第二个字符a，Trie 中没有根到a的边，跳过；
3. 看第三个字符s，Trie 中有根到s的边，跳到s，再看第四个字符h，Trie 有当前节点（写着s的那个）到h的边，跳到h，以此类推，最后跳到e，e是单词节点，并且e没有儿子，完成匹配；
4. 再回到第四个字符h，从根跳到h，再看第五个字符e，跳到e，e是单词节点，说明主串能和he匹配，再看第六个字符r跳到r，r是单词节点，并且r没有儿子，完成匹配。
5. 后面的均无法匹配，不再赘述。

AC自动机

观察上面的朴素做法过程，可以发现，我们每次匹配都要回到根节点重新匹配，这很像暴力字符串匹配每次必须回到主串的某一位置开始比较。所以我们可以借鉴KMP的思想，构建一个fail数组（KMP中也叫next数组），表示在当前节点失配后，应当去哪个节点继续匹配，而不是回到根节点浪费时间。这就是AC自动机。

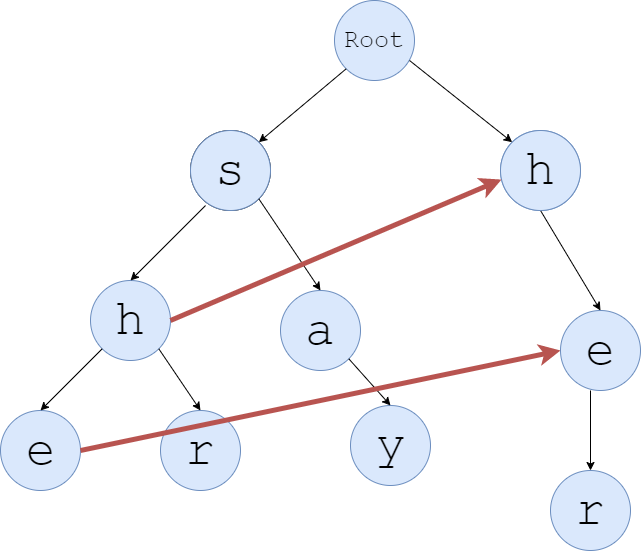
图中的红色边表示fail数组，由于除了两条红色边的起点之外，所有节点的fail都是 $0$（根节点），所以没画出来。

fail边的含义是，$\text{fail}[u]$ 为满足根到 $v$ 上的字符串是根到 $u$ 上的字符串的后缀最深的 $v$​。比如图中，h是sh的后缀，he是she的后缀。

我们先不管fail怎么求，先考虑这个求出来有什么用。

显然，在Trie暴力匹配的例子时，我们在匹配完成she这个单词后可以沿着fail边跳到e节点，和he完成匹配（因为fail数组的定义是后缀，所以既然能和she完成匹配，那一定能和he匹配，）最后又跳到r，和her完成匹配。

再举个例子：

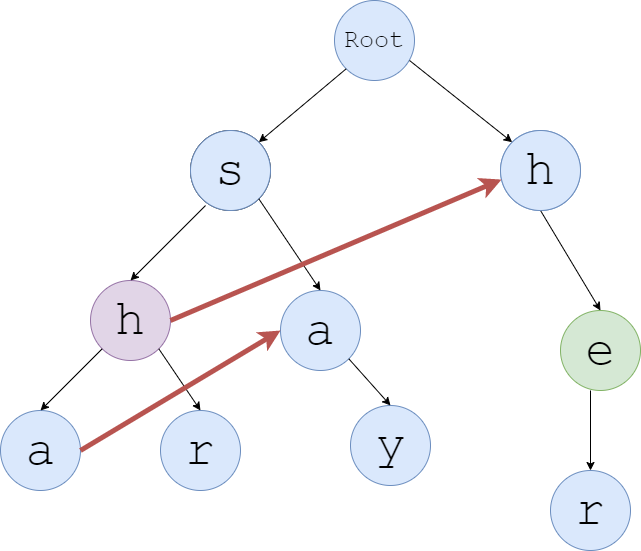
匹配到sh（走到紫色节点）时，我们发现失配了——紫色节点没有e儿子。于是选择跳fail边，跳到深度为 $1$​ 的h节点，这个时候发现和he匹配成功，并顺便匹配到了her。

接下来考虑fail数组的建立。

儿子的fail要用到父亲的fail，所以我们需要用bfs求解。ch表示儿子，则核心代码就是fail[ch[u][i]]=ch[fail[u]][i]这一行。

//构建fail数组，其中根节点为0号
void GetFail() {
	for (int i = 0; i < 26; ++ i)
		if (ch[0][i]) Q.push(ch[0][i]);
	while (Q.size()) {
		int u = Q.front();
		Q.pop();
		for (int i = 0; i < 26; ++ i)
			if (ch[u][i]) fail[ch[u][i]] = ch[fail[u]][i], Q.push(ch[u][i]);
	}
}

实际上，这样的AC自动机是一个NFA而不是DFA，在做一些AC自动机上dp之类的题目时很不方便。所以我们要把它转成DFA。

Trie图

在第二个失配的例子时，我们先从深度为二的h节点跳到了深度为1的h节点，再跳到了e节点，那为何不一步到位而非要跳两次呢？

失配的原因是紫色点没有e儿子，那我们就直接把绿色点当作紫色点的e儿子！

这样构建出来的AC自动机有一个别称叫Trie图，它是一个DFA，而且绝大多数情况能代替原来的NFA AC自动机，并且使得各种操作方便得多。

构建Fail数组的代码上，仅仅加了一行else：

void GetFail() {
	for (int i = 0; i < 26; ++ i)
		if (ch[0][i]) Q.push(ch[0][i]);
	while (Q.size()) {
		int u = Q.front();
		Q.pop();
		for (int i = 0; i < 26; ++ i)
			if (ch[u][i]) fail[ch[u][i]] = ch[fail[u]][i], Q.push(ch[u][i]);
        	else ch[u][i] = ch[fail[u]][i];
	}
}

以上讲的都是构建Fail数组，考虑怎么查询一个主串与哪些模式串匹配。

用now表示当前节点，则只需要扫描主串，让now不停地跳到它的儿子节点，那么当前和根节点到now路径上的字符串匹配成功，而且和根到fail[now]上的字符串也匹配成功，所以只需要反复跳fail边即可。

//s表示主串，cnt[i]表示以i节点作为结尾的模式串个数
for (int i = 1; i <= len; ++ i) {
		now = ch[now][s[i] - 'a'];
		for (int j = now; j && cnt[j] != -1; j = fail[j])
		    ans += cnt[j], cnt[j] = -1;//将cnt置为-1防止重复计算
	}

题目

P3041 [USACO12JAN]Video Game G

AC自动机套dp。

$f_{i,j}$ 表示按了 $i$ 个键，当前状态最后 $15$ 个字符为 $j$ 时的最大得分。

然后直接状压会爆炸，所以把 $j$ 改为 AC自动机上的一个节点，AC自动机上的状态数很少，可以通过。

#include <cstdio>
#include <queue>
#include <cstring>

std::queue<int> Q;
int ch[5005][26], fail[5005], cnt[5005], f[5005][1005], tot, len, root;
char tmp[55];
void insert(int O,int p){if(p>len){++cnt[O];return;}insert(ch[O][tmp[p]-'A']?ch[O][tmp[p]-'A']:ch[O][tmp[p]-'A']=++tot,p+1);}
void GetFail() {
	for (int i = 0; i < 26; ++ i)
		if (ch[root][i]) fail[ch[root][i]] = root, Q.push(ch[root][i]);
	while (Q.size()) {
		int u = Q.front();
		Q.pop();
		for (int i = 0; i < 26; ++ i)
			if (ch[u][i]) fail[ch[u][i]] = ch[fail[u]][i], Q.push(ch[u][i]);
			else ch[u][i] = ch[fail[u]][i];
		cnt[u] += cnt[fail[u]];
	}
}

int main() {
	tot = root = 0;
	int n, k, ans = 0;
	scanf("%d%d", &n, &k);
	for (int i = 1; i <= n; ++ i) {
		scanf("%s", tmp + 1);
		len = strlen(tmp + 1), insert(root, 1);
	}
	GetFail();
	memset(f, ~0x3f, sizeof f);
	for (int i = 0; i <= k; ++ i) f[i][root] = 0;
	for (int i = 1; i <= k; ++ i) {
		for (int j = 0; j <= tot; ++ j)
			for (int x = 0; x < 3; ++ x)
				f[i][ch[j][x]] = std::max(f[i][ch[j][x]], f[i - 1][j] + cnt[ch[j][x]]);
	}
	for (int i = 0; i <= tot; ++ i) ans = std::max(ans, f[k][i]);
	printf("%d", ans);
	return 0;
}