zqs`s blog

有朋自远方来，虽远必诛

Trie

发表于 分类于 Valine：

普通Trie

UVA11732 “strcmp()” Anyone?

把每个单词插入到一颗 trie 里面，然后对 trie 的每个节点统计一下经过该节点的单词个数，就可以统计出所有到当前节点的这一位相等，但之后的部分不相等的所有字符串的两两比较次数，最后统计答案时扫描整颗 trie 即可。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <cstdio>
#define CH tree[O].ch[ID(str[pos])]

int ID(char ch) {
	if ('0' <= ch && ch <= '9') return ch - '0';
	if ('a' <= ch && ch <= 'z') return ch - 'a' + 10;
	if (ch != '\0') return ch - 'A' + 36;
	return 62;
}
char str[1005];
long long ans;
struct Trie {
	struct Node {
		char s;
		int word;
		int ch[63];
	} tree[4000005];
	int tot;
	void insert(const int O, const int pos) {
		if (!CH) CH = ++ tot;
		tree[CH].s = str[pos], ++ tree[CH].word;
		if (str[pos] != '\0') insert(CH, pos + 1);
	}
	void find(const int O) {
		ans += tree[O].word * (tree[O].word - 1);
		tree[O].word = 0;
		int sum(0);
		for (int i(0); i <= 62; ++ i)
			if (tree[O].ch[i]) {
				const int ch(tree[O].ch[i]);
				ans += 1LL * tree[ch].word * sum, sum += tree[ch].word;
				find(ch), tree[O].ch[i] = 0;
			}
	}
} tree;

int main() {
	int n, kase(0);
	while (scanf("%d", &n) != EOF && n) {
		tree.tot = 1, ans = 0LL;
		for (int i(1); i <= n; ++ i) {
			scanf("%s", str);
			tree.insert(1, 0);
		}
		tree.find(1);
		printf("Case %d: %lld\n", ++ kase, ans);
	}
	return 0;
}

01Trie

所谓 01Trie，其实就是把每个数当成了一个01串，可以处理很多异或方面的问题还可以当平衡树用

它和权值线段树相比的优势在于常数更小，空间占用也更小。

HDU4285 Xor Sum

模板题，把每棵树当作一个01串插入到 trie 中，查询的时候考虑一个贪心：

我们优先选择最高位和查询数字不同的，再考虑次高位，在考虑第三高位……按照这个贪心原则搞就好了，我写的是递归，其实改成迭代常数小得多。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <cstdio>
#include <cstring>
#define int long long

inline int min(const int x, const int y) {return x < y ? x : y;}
int s[100005], ch[3000005][2], value[3000005], n, m, l, r, ans, ret, tot;
int query(int O, int x, int _bit) {
	if (_bit == -1) return 0;
	if (x & (1LL << _bit)) {
		if (ch[O][0]) return query(ch[O][0], x, _bit - 1);
		else return query(ch[O][1], x, _bit - 1) + (1 << _bit);
	} else {
		if (ch[O][1]) return query(ch[O][1], x, _bit - 1) + (1 << _bit);
		else return query(ch[O][0], x, _bit - 1);
	}
}
void insert(int O, int x, int _bit) {
	if (_bit == -1) return;
	if (x & (1LL << _bit)) insert(ch[O][1] ? ch[O][1] : ch[O][1] = ++ tot, x, _bit - 1);
	else insert(ch[O][0] ? ch[O][0] : ch[O][0] = ++ tot, x, _bit - 1);
}

signed main() {
	int T, kase = 0;
	scanf("%lld", &T);
	while (T --) {
		tot = 1;
		memset(ch, 0, sizeof ch);
		scanf("%lld%lld", &n, &m);
		for (int i = 1; i <= n; ++ i) {
			scanf("%lld", s + i);
			insert(1, s[i], 33);
		}
		printf("Case #%lld:\n", ++ kase);
		while (m --) {
			int x;
			scanf("%lld", &x);
			printf("%lld\n", query(1, x, 33));
		}
	}
	return 0;
}

可持久化Trie

Trie的可持久化，和主席树是一个道理，都是重复利用之前的节点，但代码非常精简。

盗图方便理解：

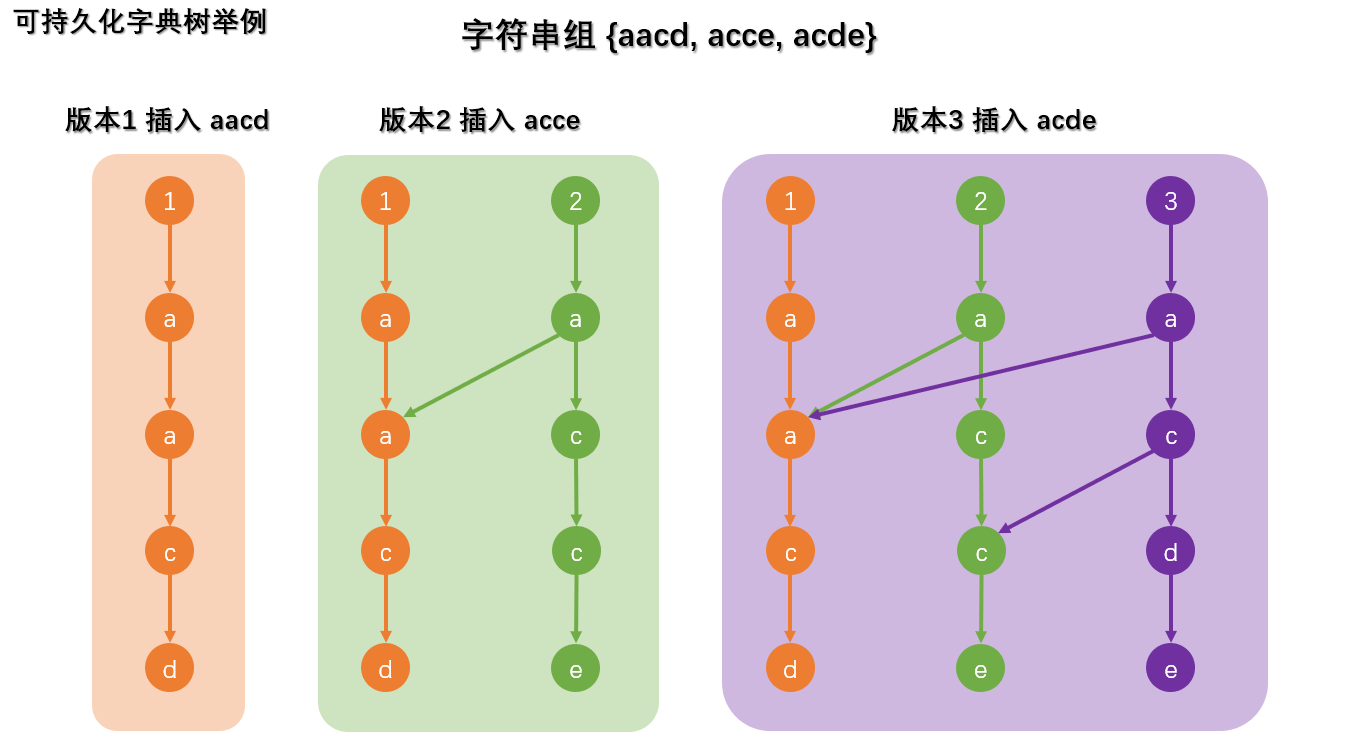
20181209112435987.png (1346×743) (csdnimg.cn)

P6088 [JSOI2015]字符串树

对于每个点都建立一颗 trie，里面存储着所有从根节点到这个节点路径上的字符串，查询的时候在 $u,v$​ 中查询答案，再减去 lca 答案的二倍。

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <cstdio>
#include <cstring>

int fa[100005][20], root[100005], ch[2000005][26], Cnt[2000005], cnt;
char str[100005][11], tmp[11];
struct Edge {
	int to, nxt;
	char str[11];
} e[200005];
int head[100005], dep[100005], n, tot, len, Tot;
inline void AddEdge(int u, int v) {
	e[++ tot].to = v, e[tot].nxt = head[u], head[u] = tot;
	int len = strlen(tmp + 1);
	for (int i = 1; i <= len; ++ i) e[tot].str[i] = tmp[i];
}

void insert(int u, int v, int x, int p) {
	if (p > len) {Cnt[u] = Cnt[v] + 1; return;}
	for (int i = 0; i < 26; ++ i) ch[u][i] = ch[v][i];
	insert(ch[u][str[x][p] - 'a'] = ++ Tot, ch[v][str[x][p] - 'a'], x, p + 1);
	Cnt[u] = Cnt[v] + 1;
}
int query(int O, int p) {
	for (int i = 1; i <= p; ++ i) O = ch[O][tmp[i] - 'a'];
	return Cnt[O];
}
void dfs(int u) {
	if (u != 1) len = strlen(str[u] + 1), insert(root[u], root[fa[u][0]], u, 1);
	dep[u] = dep[fa[u][0]] + 1;
	for (int i = 1; i <= 18; ++ i) fa[u][i] = fa[fa[u][i - 1]][i - 1];
	for (int i = head[u]; i; i = e[i].nxt)
		if (e[i].to != fa[u][0]) {
			int v = e[i].to, len = strlen(e[i].str + 1);
			for (int j = 1; j <= len; ++ j) str[v][j] = e[i].str[j];
			fa[v][0] = u, dfs(v);
		}
}
int LCA(int u, int v) {
	if (dep[u] < dep[v]) u ^= v ^= u ^= v;
	int tmp = dep[u] - dep[v];
	for (int i = 0; i <= 18; ++ i)
		if (tmp & 1 << i) u = fa[u][i];
	if (u == v) return u;
	for (int i = 18; i >= 0; -- i)
		if (fa[u][i] != fa[v][i]) u = fa[u][i], v = fa[v][i];
	return fa[u][0];
}

int main() {
	scanf("%d", &n);
	for (int i = 1; i < n; ++ i) {
		root[i] = ++ Tot;
		int u, v;
		scanf("%d%d %s", &u, &v, tmp + 1);
		AddEdge(u, v), AddEdge(v, u);
	}
	root[n] = ++ Tot;
	dfs(1);
	int q;
	scanf("%d", &q);
	while (q --) {
		int u, v;
		scanf("%d%d %s", &u, &v, tmp + 1);
		len = strlen(tmp + 1);
		printf("%d\n", query(root[u], len) + query(root[v], len) - 2 * query(root[LCA(u, v)], len));
	}
}

可持久化01Trie

如果看懂了上面三种 trie 可持久化 01trie 其实是个很自然的东西，不用我多解释了。

BZOJ3689 异或之

和 NOI2010 的那道超级钢琴一样，把每个 $i$ 对应的最小的 $a_i\oplus a_j$ 放到一个堆里面，然后每次堆 pop 一个 $i$ 后，又插入第二小的 $a_i\oplus a_j$……以此类推，重点在于如何求出 $i$ 固定，$i<j$ 时，第 $k$ 小的 $a_i\oplus a_j$。

第 $k$ 小这个条件可以直接 trie 上二分，具体过程为对每个 trie 节点记录经过该节点的数个数，如果 $k$ 小于这个个数，那么递归进入异或值较小的那一棵子树，否则进入较大的那颗子树。

区间第 $k$ 小，我们做区间第 $k$ 小数的时候把线段树换成了主席树，这里就把 01trie 换成了可持久化 01trie。

ps：想一想其实这个题用不着可持久化，直接用全局的 trie 就可以了，但可持久化 01trie 甚至比普通 trie 还好写，比 01trie 也多不了几行代码，所以我就强行把它当作可持久化 01trie 的例题了（（（

代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include <cstdio>
#include <queue>
#define int long long

typedef std::pair<int, int> PII;
int n, k, a[100005], root[100005], ch[50000005][2], cnt[10000005], kth[100005], tot;
std::priority_queue<PII, std::vector<PII>, std::greater<PII> > Q;
void insert(int u, int v, int x, int _bit) {
	if (_bit == -1) {cnt[u] = cnt[v] + 1; return;}
	if (x & (1LL << _bit)) {
		ch[u][0] = ch[v][0];
		insert(ch[u][1] = ++ tot, ch[v][1], x, _bit - 1);
	} else {
		ch[u][1] = ch[v][1];
		insert(ch[u][0] = ++ tot, ch[v][0], x, _bit - 1);
	}
	cnt[u] = cnt[v] + 1;
}
int query(int u, int v, int x, int _bit, int k) {
	if (_bit == -1) return 0;
	if (x & (1LL << _bit)) {
		if (k <= cnt[ch[u][1]] - cnt[ch[v][1]])
			return query(ch[u][1], ch[v][1], x, _bit - 1, k);
		else return query(ch[u][0], ch[v][0], x, _bit - 1, k - cnt[ch[u][1]] + cnt[ch[v][1]]) + (1 << _bit);
	} else {
		if (k <= cnt[ch[u][0]] - cnt[ch[v][0]])
			return query(ch[u][0], ch[v][0], x, _bit - 1, k);
		else return query(ch[u][1], ch[v][1], x, _bit - 1, k - cnt[ch[u][0]] + cnt[ch[v][0]]) + (1 << _bit);
	}
}

signed main() {
	scanf("%lld%lld", &n, &k);
	for (int i = 1; i <= n; ++ i) {
		scanf("%lld", a + i);
		insert(root[i] = ++ tot, root[i - 1], a[i], 32);
	}
	for (int i = 1; i < n; ++ i)
		Q.push(std::make_pair(query(root[n], root[i], a[i], 32, kth[i] = 1), i));
	while (k --) {
		int u = Q.top().second;
		printf("%lld ", Q.top().first);
		Q.pop();
		if (kth[u] < n - u)
			Q.push(std::make_pair(query(root[n], root[u], a[u], 32, ++ kth[u]), u));
	}
}
-------------本文结束感谢您的阅读-------------