题解 【NKOJ8136 买酒卖酒】

何老板在某国旅行，该国盛产葡萄酒。
沿着在一条笔直公路分布有 $n$ 个葡萄酒酒庄，酒庄编号 $1…n$。

该国针对不同的酒庄，有着不同的买卖规定。比如在 $i$ 号酒庄生产了 $P_i$ 升酒，但在 $i$ 号酒庄最多能卖掉 $S_i$ 升酒。
对于编号 $i,j$ 的两个酒庄，如果 $i<j$，则允许最多 $c$ 升酒从酒庄 $i$ 运送到酒庄 $j$。注意只能从编号小的酒庄运到编号大的酒庄。可以在多个酒庄间按任意顺序运送酒。

何老板想知道，这些酒庄，总共最多能卖出多少升酒。

---

很容易想到一个暴力的最大流：从源点 $S$ 向每个酒庄连容量为 $P_i$ 的边，从每个酒庄向源点 $T$ 连容量为 $S_i$ 的边。

若 $i<j$，从酒庄 $i$ 向酒庄 $j$ 连一条边权为 $c$ 的边，可以获得30pts。

考试的时候线段树优化建图乱搞到了70pts（

然而这个题的网络流模型非常简单，似乎直接用通用的最大流算法有点浪费。

由于最大流=最小割，所以转换为最小割问题（显然用其它方法在定义上最小割比最大流好求多了）。

考虑 dp，对于每个点都要选择放到 $S$ 集合中 $T$ 集合中。若我只选了前 $3$ 个点分到 $S$ 集合/$T$ 集合里面去。

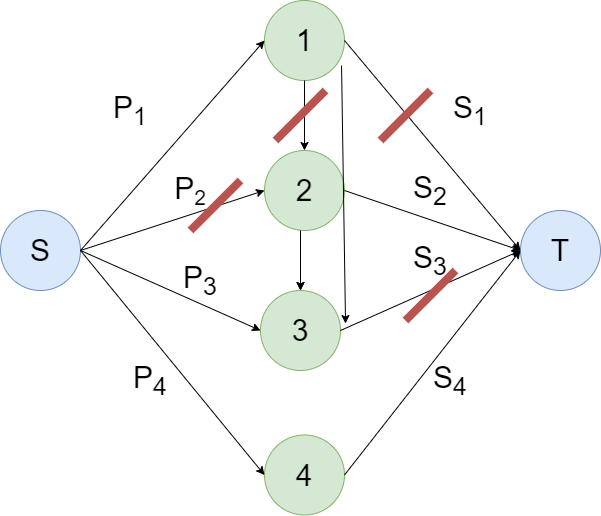
要割掉的边就是红色线划掉的边。(有一些容量为 $c$ 的边没画出来)

如果我要让 $4$ 到 $T$ 集合，那么除了割掉 $P_4$ 以外还要割掉 $1\rightarrow 4,3\rightarrow 4$ 这些容量为 $c$ 的边。换言之，假设我已经选了 $j$ 个点在 $S$ 集合，如果当前点要在 $T$ 集合，则需要割掉 $j$ 条容量为 $c$ 的边。

如果我要让 $4$ 到 $S$ 集合，则只需要割掉 $S_4$ 这条边。

那么定义状态：$f_{i,j}$ 表示前 $i$ 个点有 $j$ 个分到了 $S$ 集合，则转移为：

$f_{i,j}=\min(f_{i-1,j-1}+S_i,f_{i-1,j}+P_i+j\times c)$。

需要用滚动数组优化空间，代码奇短。但思维难度可谓是非常大。

#include <cstdio>
#include <cstring>
#define int long long

inline int min(const int x, const int y) {return x < y ? x : y;}
int f[2][10005], p[10005], s[10005], n, c, ans = 1e18;

signed main() {
	memset(f, 0x3f, sizeof f);
	f[0][0] = 0;
	scanf("%lld%lld", &n, &c);
	for (int i = 1; i <= n; ++ i) scanf("%lld", p + i);
	for (int i = 1; i <= n; ++ i) scanf("%lld", s + i);
	for (int hhh = 1, i = 1; hhh <= n; ++ hhh, i ^= 1) {
		f[i][0] = f[i ^ 1][0] + p[hhh]; 
		for (int j = 1; j <= hhh; ++ j)
			f[i][j] = min(f[i ^ 1][j - 1] + s[hhh], f[i ^ 1][j] + p[hhh] + j * c);
	}
	for (int i = 0; i <= n; ++ i) ans = min(ans, f[n & 1][i]);
	printf("%lld", ans);
	return 0;
}