题目大意：

给你一颗 $n$ 个点构成的树，要在这棵树上选择 $m$ 条互不相交的链，求这些链中长度最小的最大长度。

题目分析：

算法主框架

看到这种类似要求”最小值最大”或者”最大值最小”，首先就应该想到二分这个最小值或最大值。

对于本题，二分最短的赛道长度 $lim$。为了方便后文描述，$cnt$ 表示当前找到的满足限制的赛道条数。

二分上界：$\sum l_i\div m$。

如何检查二分的值是否能够实现

我们知道，一条赛道不可能同时经过一个节点的两颗以上的子树。对于一颗子树，我们先找到在这颗子树内的所有的长度大于等于 $lim$ 的赛道，再没被经过的其它边中找一条最长的链，把这条链的长度向上（它的父亲）传递。

什么意思呢？拿样例一来说：

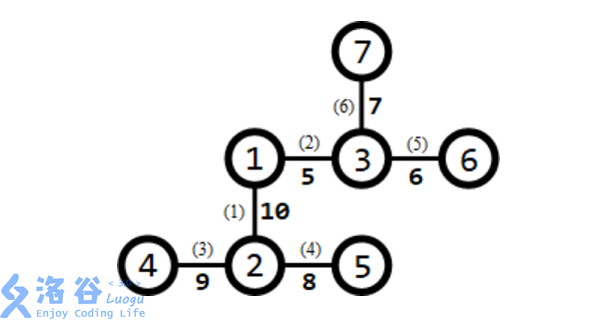
我们设 $7$ 为树的根，设当前二分的 $lim=19$，则 $4$ 没有任何儿子，向它的父亲 $2$ 上传递 $0$。$5$ 没有儿子，向 $2$ 传递 $0$。这个时候，$2$ 将这些传递的值加上对应的边权，这些值就变成了 $8,9$。
这个时候，肉眼观察发现 $8$，$9$ 都不满足条件，将这两个值加起来 $8+9=17<19$ 也不满足条件。而我们只能向上传递一条最长的链，于是向 $1$ 传递值 $9$。$1$ 将这个值加上边权 $10$，得到 $19$。
这个时候，我们发现 $19$ 满足条件。那么把这个向上传递的值删除，因为它满足了条件，我们即使把它向上传递，$cnt$ 最多也是加1，还不如就地用了直接报废，给上面多留一些边。那么此时 $1$ 没有可以传递的值了，向 $3$ 传递 $0$，加上边权变为 $5$。

然后这个时候 $3$ 除了 $1$ 这个儿子，又找到 $6$ 向它交代。$6$ 没有任何儿子，传递 $0$。加上边权 $6$ 就是 $6$。$3$ 最终有两个元素：$5$ 和 $6$。这两个元素加起来都不够 $19$，向 $7$ 传递 $6$，加上边权为 $13$。
7发现没有其它儿子，$12<lim$，就地报废。最终，$cnt=1$，所以当 $lim=19$ 时，最多能修建 $1$ 条长度大于等于 $19$ 的赛道。

总结一下：

从根节点出发向下dfs，让它的儿子向它传递值。
将它的儿子传递上来的值加上边权，从小到大排个序，从最小值开始扫，找到能和它配对（也就是与它的和大于等于 $lim$）的值时删除这两个元素，$cnt++$。很显然，这个过程用multiset比较合适。代码中为每个节点都分配了一个multiset。
在 multiset 中剩下的元素中找最大的，如果为空就往父节点传递0（代码为return 0，否则返回集合中最大的元素。）

这道题的分析就完了。解释一下代码：dfs(u,f)表示当前搜索到节点 $u$，父节点为 $fa$，让它向父节点传递值。

注意：每次二分后cnt要重置为0，每个点的multiset都要清空！（我在这里卡了两个小时希望没把你吓到）。

时间复杂度 $O(nlog(\sum l_i\div m)log n)$。

$Code:$

#include <cstdio>
#include <set>

struct Edge {
int to, v, nxt;
} e[100005];
int head[50005], tot, lim, cnt;
std::multiset<int> sons[50005];
inline void AddEdge(int u, int v, int w) {
e[++ tot].to = v, e[tot].nxt = head[u], head[u] = tot, e[tot].v = w;
}

inline int dfs(int u, int fa) {
std::multiset<int>& s(sons[u]);
for (int i(head[u]); i; i = e[i].nxt)
if (e[i].to != fa) {
int w(dfs(e[i].to, u) + e[i].v);
if (w < lim) sons[u].insert(w);
else ++ cnt;
}
if (s.empty()) return 0;
for (auto i(s.begin()); i != s.end();) {
auto it(s.lower_bound(lim - *i));
if (i == it) ++ it;
if (it != s.end()) {
++ cnt, s.erase(i ++);
if (i != it) s.erase(it);
else s.erase(i ++);
}
else ++ i;
}
return s.empty() ? 0 : *(-- s.end());
}

int main() {
int n, m, l(1), r(0), ans(0);
scanf("%d%d", &n, &m);
for (int i(1); i < n; ++ i) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
AddEdge(u, v, w), AddEdge(v, u, w), r += w;
}
r /= m;
while (l <= r) {
lim = l + r >> 1;
for (int i(1); i <= n; ++ i) sons[i].clear();
cnt = 0, dfs(1, -1);
cnt >= m ? ans = lim, l = lim + 1 : r = lim - 1;
}
printf("%d", ans);
}

zqs`s blog

洛谷P5021 【NOIP2018D1T3】赛道修建